La dupli del cubo

Cara frateles[¹],

Nos vade a parla oji de la problem jeometrial nonsolveda 3 de la Anticia: la dupli de la cubo.

Como me ia dise ja, a la comensa de nosa parlas, cuando nos ia trata la trisesioni del angulo, un problem incluinte un egali de la grado 3 no es solvable apriori con regla e compas, en la spasio bidimensional de un folia. Par esta causa, Alzon, en sua construis, ia inclui un dimension 3: la tempo. En fato, si on ajunta la dimension de tempo a la du dimensiones de la folia plana, esta problem de grado 3 deveni solvable!

Nos va vide ce Alzon, un disiplo umil de Pandrosion (un fem matematiciste en la sentenio 4 ec.), ia proposa un solve interesante con regla e compas de la problem de la dupli del cubo, cual la edas posterior ia iniora. An Pappos la Alexandrian, sua contempora, evoca no sua nom, no sua solves tan astuta! Nos encontra sua construi sola en la obra ja sitada de dom Munius, la Opera mathematica, un obra cual es disponable sola en la biblioteca de nosa isola xef, e a no otra loca del mundo.

La ojeto

La demanda es ce, de un cubo inisial con un volum v, on construi un cubo con un volum duplida (w = 2 × v). Par causa ce on labora sur un folia de paper plata, on va construi, de la lado de la cubo peti, la lado de la cubo grande, e an trasa un fas de ambos cubos.

On calcula la volum v de la cubo prima tal, multiplinte sua lado a par lo mesma e ancora par lo mesma, tal:

E on calcula la volum w de la cubo grande tal, multiplinte sua lado b par lo mesma e, a un ves plu, par lo mesma, tal:

Ta ce (b : a) es r; donce b = r × a

E, afin la volum es duplida:

On debe trova un ratio r tal ce

La metodo

Dom Munius nota ce la metodo de Alzon per dupli un cubo es fundida sur la construi de la promedia jeometrial entre du longias.

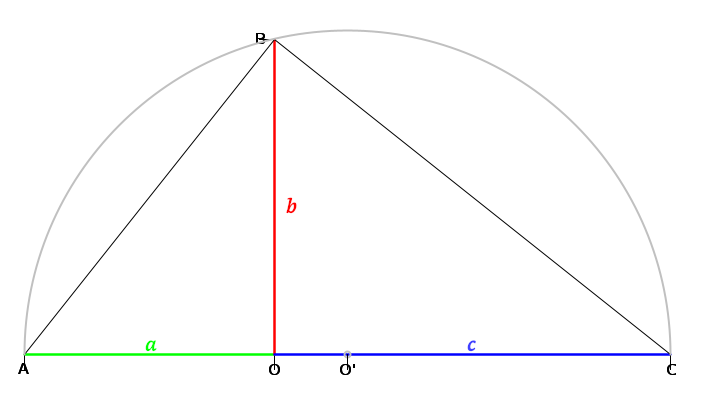
En acel desinia, la triangulos AOB e BOC es simil. La ratio (OB:OA) es egal a la ratio (OC:OB). La longia OB es la promedia jeometrial entre OA e OC. Si on nomi a la longia OA, b la longia OB e c la longia OC, on pote scrive ce (b:a) = (c:b) = r, e ce b² = ac (cual es la defini de la promedia jeometrial).

Si on dona a c la valua 2a, alora:

Tal, on ia dupli la valua de a tra du creses identica.

Ma la ojeto de Alzon es susede dupli la valua de a tra tre creses identica. El imajina la ajunta de un construi identica (ma vertical), per oteni la promedia jeometrial entre OB e OD, a esta ves. En acel ajunta, la triangulos BOC e COD es simil. La ratio (OC:OB) es egal a la ratio (OD:OC). La longia OC es la promedia jeometrial entre OB e OD, per dise c² = bd. Tal es la imaje ce on debe ave, final:

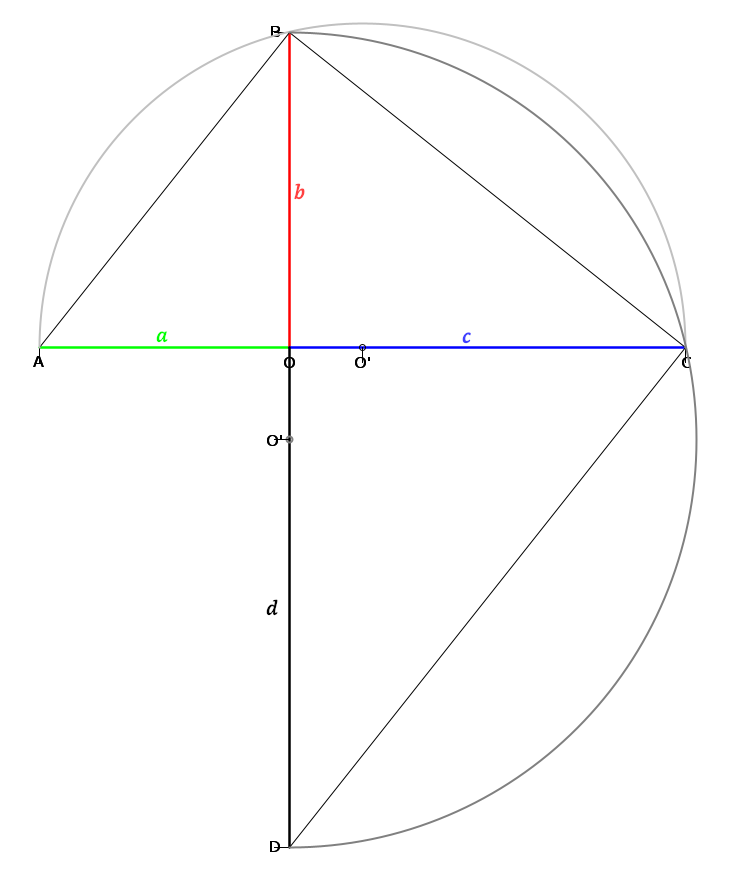
Tal, la triangulos AOB, BOC e COD es simil. La ratios (OB:OA), (OC:OB) e (OD:OC) es egal. Si on nomi d la longia OD, on pote scrive: (b:a) = (c:b) = (d:c) = r.

Si on dona a d la valua 2a, alora:

La volum de la cubo con un lado ra ave la valua (ra×ra×ra) =  (r×r×r) × (a×a×a) = 2a³, per dise un volum duplida.

La construi jeometrial de la dupli del cubo

Alzon comensa con la desinia de un cuadro cual es la fas de la cubo inisial, con un lado AO = a, a sinistra de la punto O. Poi, sur la linia reta AO, a destra de O, el trasa la segmento OC₀, con un longia c₀ = 2a. En la parte inferior de la desinia, sur la ase vertical, el trasa la segmento OD = 2a.

Alora, Alzon aplica esta algoritmo sur la puntos A e C₀:

1. Sur la diametro AC₀, el trasa un arco de 180°; la crusa de la arco con la parte superior de la ase vertical locali la punto B₀. La triangulos AOB₀ e B₀OC₀ es simil, como nos ia vide en la imaje prima.
2. Poi el trasa sur la diametro B₀D un arco de 180° ; la crusa de la arco con la parte destra de la ase orizonal locali la punto C₁; la longia de la segmento OC₁ es c₁.

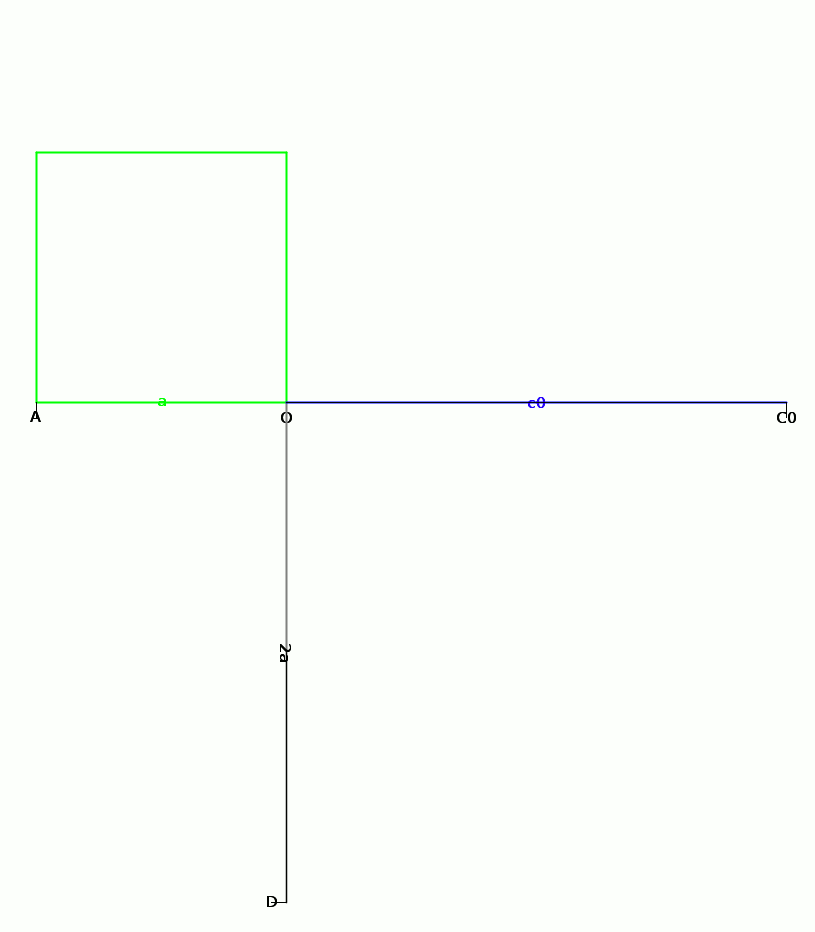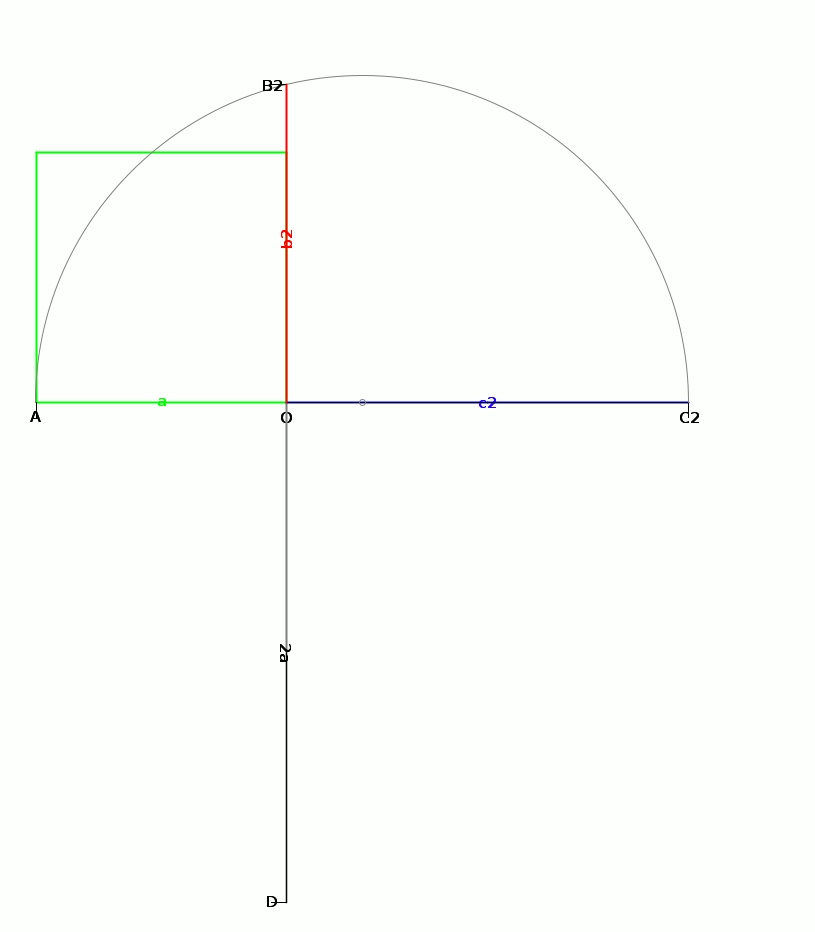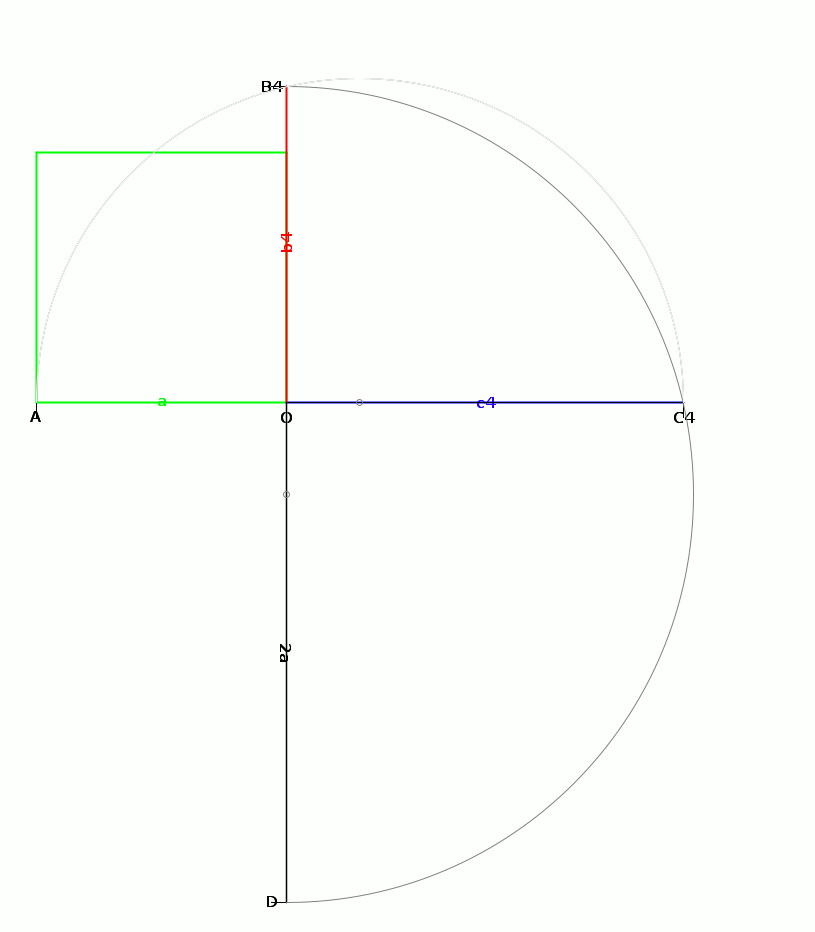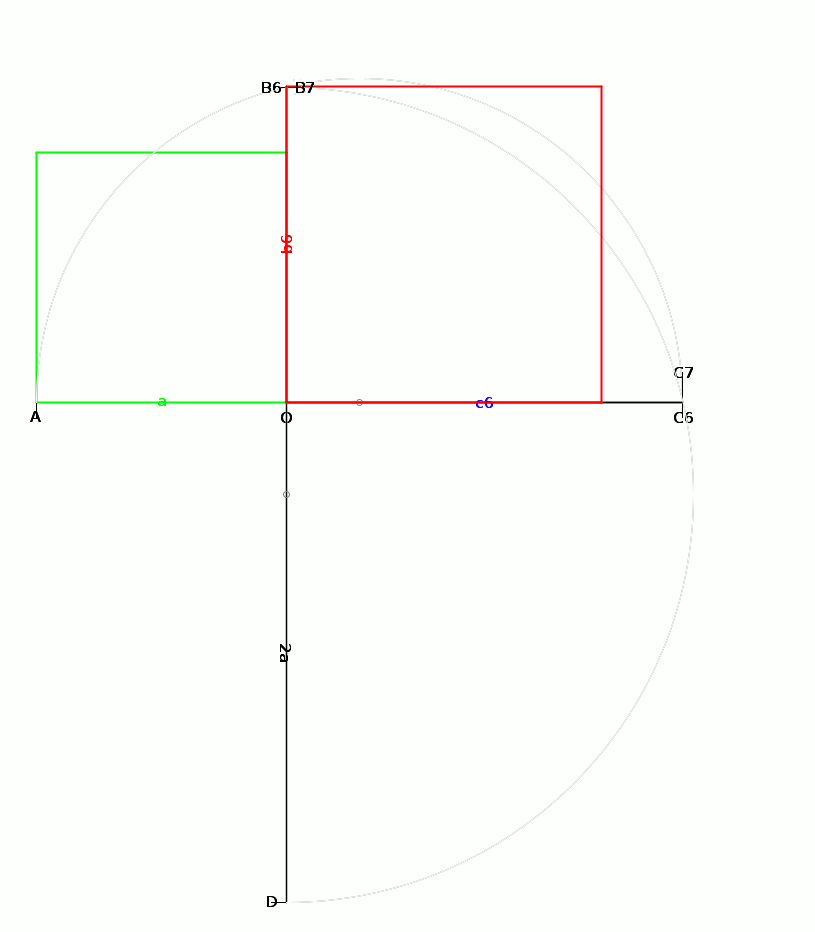
On nota ce la puntos C₁ e C₀ no fusa en lunlotra. Ma, si on aplica la algoritmo jeometrial sur la puntos A e C₁, on oteni un punto B₁, poi un punto C₂. On nota alora ce la puntos C₂ e C₁ prosimi a lunlotra.

A cada ves, la algoritmo recomensa de la punto A e de un punto Cₙ per ateni un punto Bₙ, poi un punto Cₙ₊₁. Gradal, la puntos Cₙ₊₁ e Cₙ prosimi plu e plu a lunlotra [²], asta ce la spesia de la stilo covre la du puntos, cual fusa en lo. Alora la prosede fini.

On trasa final la fas de la cubo nova sur la lado OB, per dise la cuadro roja: la cuadro verde es la fas de la cubo inisial, e la cuadro roja es la fas de la cubo final con un volum duplida relatada a la cubo inisial. Lo cual on ia vole mostra.

Cara frateles onorable, me ia parla.